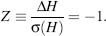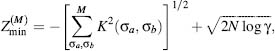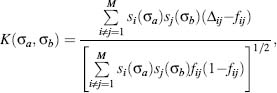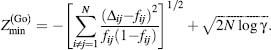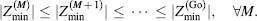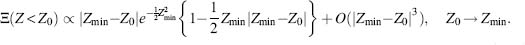39
PROTEIN DESIGNABILITY AND ENGINEERING
INTRODUCTION
Rapid scientific and technological advances in biological sciences that started in the second half of the twentieth century have led to exploration and engineering at the scale of single biological molecules. DNA manipulation techniques, such as polymerase chain reaction (PCR), allowed almost arbitrary control of proteins that are expressed in living cells. These developments prompted scientists to ask increasingly ambitious questions pertaining to cell life, evolution, and the molecular origins of diseases. Rational manipulation of protein function through alteration in sequence and structure became an important aspect in the quest to answer these questions.
A protein’s sequence uniquely defines its three-dimensional structure. This relationship is perhaps the most central paradigm of protein biophysics. Interestingly, however, a protein structure does not uniquely define a single sequence: multiple sequences often correspond to similar protein structures. This aspect turned out to be central for the field of structural bioinformatics. Similarly, a protein’s structure defines its function, although a given structure can have several biological functions. Hence, one approach to manipulate protein function is through its sequence. Nature diversifies protein function through sequence over the course of evolution. This process is often referred to as protein evolution. Understanding protein evolution has become an important subject because of the temptation to manipulate protein function through rational alternation in protein structure via its sequence. This process is referred to as protein design or protein engineering, although the latter term has a grander-scale connotation, best applicable to more complex systems such as protein-protein or protein-DNA complexes.
How can the manipulation of protein function help in understanding cellular life and the molecular origins of diseases? The most obvious applications are direct examinations of how protein function alterations are coupled to phenotypic or symptomatic outcomes. More complex applications include various biosensors engineered to “sense” various target proteins’ states, protein-protein interactions, protein cellular localization, and expression levels. Potential therapeutic applications of protein engineering also include design of novel antibodies and biomarkers to proteins that are elevated during a disease state with respect to the healthy state.
The appeal of protein structure-function manipulation led to a number of studies pertaining to questions about the possibilities and limitations of protein engineering. Protein design is a search procedure, either computational or experimental, that aims to determine amino acid sequences that correspond to a specific structure. Perhaps, the most central question of protein design is how “designable” is a specific structure, that is, how many sequences correspond to a specific protein structure. This question, first addressed from a purely theoretical perspective, has become one of the most intriguing questions in protein evolution and design, and is the subject of this chapter.
Before turning to the discussion of designability, we first review the intrinsic properties of naturally occurring proteins, organization of the protein structural universe, key determinants of protein structure, and protein evolution. We then discuss essential requirements for and other questions pertaining to protein design. Finally, we talk about challenges in protein design.
PROTEIN STRUCTURAL UNIVERSE
An understanding of the range of protein structures that can be adopted by Nature must first be appreciated before undertaking protein engineering efforts. Protein structures are organized hierarchically as discussed in more detail in Chapter 2. Several secondary structure elements—α-helices, β-strands, hairpins, and loops—form domains, quanta of protein structure. The domains can be defined unambiguously from the thermodynamic and folding kinetics points of view. Protein domains must be able to exist on their own, that is, isolated protein domain sequences must be able to reach their native states and be thermodynamically stable. Proteins can be further built by linking multiple domains. One must appreciate the wisdom of Nature in creating such modularity in the protein universe, because modularity permits the combinatorial multiplicity of possible proteins.
The consequence of structural modularity is that protein functions are modular as well. Indeed, let us imagine a need for a protein that would respond to a specific stimulus, cross the nucleus, associate with DNA, and initiate transcriptional response to this stimulus. Such a protein can be built by incorporating the stimulus-sensing domain (e.g., binding a specific small molecule), a nuclear transport domain, a DNA binding domain (e.g., containing a Zn-finger motif), and potentially, a catalytic domain to instigate a response. The beauty of this modular design, a strategy used by Nature, is that the need to extensively explore protein sequence and structural space is reduced. Instead, the selection and combination of a few domain architectures often produce a synergistic solution to constructing a protein with a desired biological function.
Further protein assembly into functional complexes with these modular units adds new dimensions to protein function. Thus, protein function is also hierarchical (Anantharaman, Aravind, and Koonin, 2003; Shakhnovich et al., 2003) and can be defined at multiple levels of protein structure: from the domain level to the level of molecular complexes. Perhaps the functional quantum of protein structure is a domain. Hence, it is plausible that evolution of proteins is dictated by the evolution of functional domains.
The question “how many protein folds exist?” has been an extremely hot topic of discussion. A number of answers have appeared, but all of them report the number of folds (NF) to range between 1000 and 10,000 (Chothia, 1992; Orengo, Jones, and Thornton, 1994; Wolf, Grishin, and Koonin, 2000). How many should we expect if Nature were to exhaustively explore all possibilities? Let us count. A typical N = 100 residue protein has Nss = 15 secondary structure elements, including strands, helices, loops, and turns. Then theoretically, NF = Nss! ~ 1012 possibilities to arrange these structural elements with respect to each other (Table 39.1). This number is significantly larger than what is observed and even projected. Hence, it is clear that either evolution has not fully explored protein fold space or some folds are not designable, or both.
Importantly, the number of structures NS that a 100-residue
protein can explore is much larger than the number of folds (NS 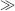 NF). To estimate NS, let us position a simplified protein model on a lattice, where each
residue is represented as vertices, with the number of adjacent lattice vertices (the coordination
number) z (for cubic lattice z = 6). The
coordination number defines the number of possible interactions between residues. With this model
neighboring residues can be positioned in (z – 1) vertices, adjacent to the current residue. Then,
there are (z – 1)(N–1) = 1099log5 ≈ 1069 possibilities to build a N = 100 residue protein structure. We ignore self-avoidance of polymer chains
(Grosberg and Khokhlov, 1997), since it is potentially compensated by our lattice considerations.
However, only a fraction of 1069 possible protein structures will be
compact. To estimate the fraction of compact proteins, we refer to a recent work by Chen, Ding, and
Dokholyan (2007) who demonstrated that on average α ≈ 1.7 proximity constrains
per residue define a protein structure within 3.5 Å root-mean-square distance from its native structure.
Then, the total number of possible structures that a 100-residue proteins can adopt is NS ≈ 1069/α99 ≈ 1047. This number corresponds to the total
number of compact 100-residue protein structures, which is also the number of sequences N∑ that correspond to compact protein structures,
that is, the number of protein sequences. Importantly, the total number of possible sequences for a
100-residue protein is 20100 ≈ 10130, much larger than the number of sequences that correspond to compact
proteins.
NF). To estimate NS, let us position a simplified protein model on a lattice, where each
residue is represented as vertices, with the number of adjacent lattice vertices (the coordination
number) z (for cubic lattice z = 6). The
coordination number defines the number of possible interactions between residues. With this model
neighboring residues can be positioned in (z – 1) vertices, adjacent to the current residue. Then,
there are (z – 1)(N–1) = 1099log5 ≈ 1069 possibilities to build a N = 100 residue protein structure. We ignore self-avoidance of polymer chains
(Grosberg and Khokhlov, 1997), since it is potentially compensated by our lattice considerations.
However, only a fraction of 1069 possible protein structures will be
compact. To estimate the fraction of compact proteins, we refer to a recent work by Chen, Ding, and
Dokholyan (2007) who demonstrated that on average α ≈ 1.7 proximity constrains
per residue define a protein structure within 3.5 Å root-mean-square distance from its native structure.
Then, the total number of possible structures that a 100-residue proteins can adopt is NS ≈ 1069/α99 ≈ 1047. This number corresponds to the total
number of compact 100-residue protein structures, which is also the number of sequences N∑ that correspond to compact protein structures,
that is, the number of protein sequences. Importantly, the total number of possible sequences for a
100-residue protein is 20100 ≈ 10130, much larger than the number of sequences that correspond to compact
proteins.
TABLE 39.1. Estimations and Observed Numbers for the Protein Universe for N = 100 Residue Long Proteins
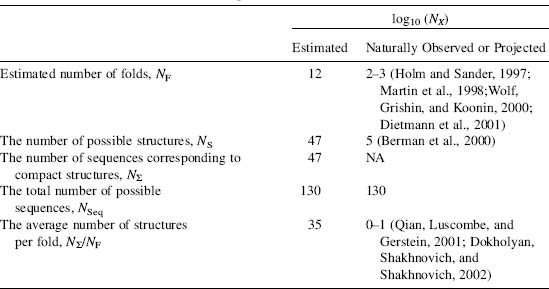
These estimations suggest that if all folds are equivalent, that is, there are equal numbers
of structures that correspond to each fold, then, there are NS/NF = N∑/NF ≈ 1035 protein structures per fold.
This assumption does not likely hold: Dokholyan, Shakhnovich, and Shaknovich (2002) reported that the
number of naturally occurring protein domains in fold families are distributed unevenly with respect to
the structures that contain them and follow a power law distribution 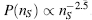 . While such an uneven distribution may suggest that some
domains are more designable than others, it may also be the result of diverging evolutionary processes.
We return to the issue of designability later in this chapter.
. While such an uneven distribution may suggest that some
domains are more designable than others, it may also be the result of diverging evolutionary processes.
We return to the issue of designability later in this chapter.
DETERMINANTS OF PROTEIN DOMAIN EVOLUTION
There are several different evolutionary factors that impact the designability of proteins. At the level of organisms, evolution optimizes adaptation of organisms to new or changing environments. This adaptation is accommodated through modifications of protein function that are achieved through changes of protein sequences and structures, or through changes in the expression levels of the proteins. Protein evolution is determined by the former modifications of protein sequence and consequent structural rearrangements. What are the factors that drive protein evolution? By examining mutational strategies and the effects of mutations in Nature, the examples will help guide our understanding of the underlying design rules that needs to be considered when addressing protein designability and engineering experiments.
Protein evolution proceeds through amino acid substitutions and fragmental rearrangements (deletions, insertions, truncations). These mutations can affect three aspects of proteins: (1) structure, (2) function, and (3) folding kinetics. If a mutation disrupts the folding kinetics of a protein, it may lead to misfolding and aggregation. There is a large number of misfolding-related disorders. Perhaps the most illustrative example is cystic fibrosis (Boucher, 2004) since 90% of all cases are attributed to a single amino acid deletion ΔPhe508 in the cystic fibrosis transmembrane conductance regulator (CFTR; Riordan et al., 1989; Rommens et al., 1989). The mutant protein’s thermodynamic stability is not perturbed and it is not functional because it never matures as a transmembrane protein, suggesting that deletion of phenylalanine affects the folding kinetics of this protein. Clearly, this example demonstrates that preservation of protein folding kinetics may be a key factor in protein evolution.
Mutations leading to a loss of protein function can often be lethal. There are numerous examples of mutations that perturb functional sites, thereby affecting organism viability (see, for example, Akiyama et al., 2007; He et al., 2007). A number of loss-of-function mutations are embryonically lethal, especially those that involve proteins that play central roles during development. These facts suggest that the preservation of protein functional sites may also be a key factor in protein evolution.
Mutations that affect the protein stability are also associated with numerous diseases. Examples include familial amyotrophic lateral sclerosis (FALS) caused by over 100 mutations in Cu, Zn superoxide dismutase 1 (SOD1; Cleveland, 1999; Khare, Caplow, and Dokholyan, 2006; Figure 39.1) and familial amyloid polyneuropathy caused by mutations in transthyretin (Benson and Kincaid, 2007). Interestingly, in the case of FALS, many SOD1 mutants are as active as wild type, but they potentially gain toxic function due to association into pathogenic oligomeric states due to destabilization. This toxic gain-of-function may be under cellular repair machinery control until this control deteriorates due to aging. If the organisms are at or past the reproductive age when disease manifests itself, they can produce offspring, therefore organism evolution is not affected significantly. Hence, it may seem that mutations that affect protein stability are not as important as those that affect protein folding kinetics or function.
Figure 39.1. Single nucleotide polymorphisms in the human Cu, Zn superoxide dismutase (SOD1) associated with the amyotrophic lateral sclerosis. Over 70 mutations are scattered throughout the tertiary structure affecting multiple structurally distinct sites, marked by colored meshes. For simplicity only one monomer of the homodimeric SOD1 is shown in two projections. Figure also appears in the Color Figure section.
Surprisingly, this is not the case. Dokholyan and Shakhnovich (2001) showed that if one attempts to mimic protein evolution through sequence alterations that preserve protein thermodynamic stability, then amino acid positions that contribute the most to stability appear the most conserved during such alterations. This observation is further supported by examining the conservation pattern obtained in synthetic evolution, which is found to closely match that is observed naturally (Dokholyan and Shakhnovich, 2001). The correlation between the naїve synthetic and observed amino acid conservations is as high as 70%, suggesting that proteins are under a dominating evolutionary pressure to preserve their structural stability. Of course, the correlation is not perfect, suggesting that the preservation of folding kinetics and function are under evolutionary pressure as well.
Why would evolution preserve residues important for structural stability in proteins? There could be several reasons. First, the number of residues that constitute either the folding nucleus or the active site of the protein is usually much smaller than those that constitute the protein core. Hence the probability that a random substitution will affect either the folding nucleus or the active site is much smaller than the probability that it will affect the protein core. Second, function itself is not conserved in the course of evolution. Although proteins belonging to a specific fold tend to share a set of functions (Shakhnovich et al., 2003), these functions can be diverse enough that the active sites are fully altered. The folding of homologous proteins can be distinct as well, as for example in the case of two homologues Im7 and Im9 (Friel, Capaldi, and Radford, 2003), suggesting that the folding nucleus may not be under strong evolutionary pressure to be preserved. Thus, among three factors—protein structure, folding kinetics, and function—the protein structure is the most invariant. Hence, residues that maintain structural stability are under evolutionary pressure.
Mutations that impact protein stability also impact protein function. Proteins that are severely destabilized upon mutation are either eliminated due to a loss of function or retained through a compensating mutation that reverses the effect by recovering their thermodynamic stabilities. Recently Bloom et al. (2006) demonstrated that improving thermodynamic stability of marginally stable cytochrome P450 increases the chances of the enzyme to exhibit new or improved function. Mildly destabilizing mutations are perhaps the most dangerous as the proteins may still be functional, but not to the extent necessary to maintain the health of the organism. A number of recent studies support the hypothesis that mildly destabilizing mutations in the human genome are the underlying genetic origin of complex diseases (Sunyaev et al., 2001; Yampolsky et al., 2005; Eyre-Walker, Woofit, and Phelps, 2006; Kryukov, Pennacchio, and Sunyaev, 2007).
Evolutionary pressure to preserve protein structure has important implications on protein design. It is plausible that Nature has found “working” folds and exploits them by grafting necessary functions on to them. If stability is preserved and the scaffold can accommodate the new active site or a binding surface, a new protein with protein function can appear. This idea has been utilized in proof-of-principle studies: Hellinga and coworkers successfully transplanted triose phosphate isomerase activity (Dwyer et al., 2004) from one ribose-binding protein to another homologous enzyme (Allert, Dwyer, and Hellinga, 2007). However, while evolution appear to select for structural preservation offolds, Nature needs new folds to explore new functional space. Consequently, evolution is abalance of forces that conserve and diversify the protein domain universe. The mechanisms of protein domain evolution are discussed next.
MECHANISMS OF PROTEIN DOMAIN EVOLUTION
Clues to protein evolution can be observed by understanding conservation patterns imprinted in the protein sequence-structure-function space (Dokholyan and Shakhnovich, 2005; Dokholyan and Shakhnovich, 2007). Protein sequences and structures (Levitt and Chothia, 1976), as well as functions, are not distributed uniformly with respect to each other when corresponding measures of similarity between sequences, structures, or functions are used. Instead, proteins tend to fall into clusters of families with sequences sharing more than 20% sequence similarity often adopting similar structure and often function. These families of proteins are typically assumed to have originated from a common ancestor. However, it is also possible for proteins with less than 10% sequence similarity to share similar structures and functions. For these instances, convergent evolution is suspected to be involved because the sequence similarity is equal to what would be expected of two randomly selected proteins (Holm and Sander, 1993; Rost, 1997).
Convergent evolution is the result of structural exploration from two distinct origins reaching an equilibrium where the structural solution for a given function is similar to each other. The argument for a convergent evolution scenario can also be presented without the assumption of equilibrium in structural exploration. In which case, a specific force X of unknown origin that selects for specific folds to perform a given function needs to be specified, rather than exploring a multiplicity of other folds for function optimization. Moreover, this force X should be universal since it helps guide the selection of many distinct families of analogues.
There are several important arguments that are at odds with the convergent evolution theory. First, the assumption of equilibrium in structural exploration is inconsistent with the estimated number of protein folds since the number of theoretically possible folds still exceeds what is observed (see discussion in Protein Structural Universe section). Second, the origin of the mysterious force X is unknown and it is not clear what would make two presumably unrelated protein structures adopt the same structure and function. An alternative model suggests that protein designability is the guiding force of evolution and can be used to explain the uneven distribution of the number of members of protein fold families. An extension of this model, and simpler explanation for this distribution, was proposed by Dokholyan, Shakhnovich, and Shakhnovich (2002) using graph theoretical analysis that does not rely on any assumption (described in more detail later). Therefore, these models argue against the missing force X in the convergent evolution theory based on the lex parsimoniae principle. Third, it is arguable that protein domains presumed to be unrelated may in fact be related, but the connection between them is lost (Pei et al., 2003). The premise for establishing evolutionary relationship is often based in the amount of sequence conservation that may not necessarily hold. Indeed, sequences have been observed to diverge rapidly below the 15% similarity threshold during the course of simulated evolution while maintaining the original protein fold.
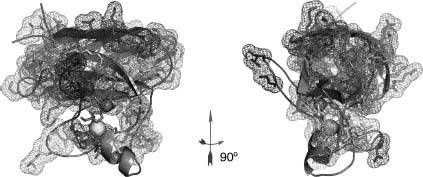
In the divergent protein evolution theory (Chothia and Gerstein, 1997; Grishin, 1997; Murzin, 1998; Zeldovich et al., 2007; Figure 39.2a) all proteins originate from a few protoproteins. The collective mutations accumulated across time create a repertoire of different proteins while maintaining their structural integrity. The current protein universe is a snapshot of the exploding protein universe. To reconstruct relationships between proteins, a comparison of sequences may not be sufficient. Structures are more conserved than sequence across a long evolutionary time and is useful to establish connections between seemingly unrelated protein domains. For some families, it may be possible to uncover connections between distinct fold families that are related by identifying proteins that can convert from one fold to another with few mutations (Cordes et al., 1999, 2000). Perhaps the most prominent example of such chameleon proteins is the dimeric α + β Cro protein from bacteriophage lambda, which evolved from an ancestral all-α monomeric protein (Figure 39.2b; LeFevre and Cordes, 2003). By retroevolving lambda Cro, Le Fevre et al. suggested possible mutations that are responsible for the evolution of the ancestral monomeric protein to the modern dimeric homologue.
The protein domain universe graph (PDUG) is constructed to map the relationships between proteins (Dokholyan, Shakhnovich, and Shakhnovich, 2002) and helps to highlight the mutational strategies used by Nature to evolve different folds. In PDUG, each node represents a protein domain and is connected by a bond that carries a weight corresponding to the degree of their structural similarity. PDUG is organized by a large number of subclusters (Figure 39.3) that serves to reflect the imprint of the evolutionary mechanisms. Examining the connectivities within the PDUG subclusters offers important insights into the appearance of new folds. Although chameleon proteins may be exceptions rather than the rule for the appearance of new folds, it is evident that there are certain proteins that play a role of a gatekeeper for specific folds. Elimination of these proteins during evolution separates connected families of protein folds, thereby giving birth to a new fold family (Dokholyan, 2005). One such example is a hydrolytic enzyme cutinase, which degrades cutin (Dokholyan, 2005). Cutin is a polyester composed of hydroxy and epoxy fatty acids, which serves as a protective shield of aerial plants against pathogen entry (Purdy and Kolattukudy, 1975). Cutin degradation is the first step for plant infection and is exploited by fungi expressing cutinase to invade plants. This unique mechanism of plant protection and infection may trace back to the very origin of plants. Coevolution of plants and pathogens may have spurred an observed spread of domains in the largest cluster of the PDUG (Figure 39.3).
Figure 39.2. Mechanism for protein structure evolution. (a) A schematic representation of the proposed mechanisms for protein evolution (Dokholyan and Shakhnovich, 2005; Dokholyan and Shakhnovich, 2007). Minor structural changes associated with point mutations in proteins diversify the fold families. Major structural changes due to accumulated mutations result in the formation of new fold families. These fold families are populated unequally, some families are represented by just a single protein (orphan family; Dokholyan, Shakhnovich, and Shakhnovich, 2002). In some cases, the proteins may adopt structures that would “bridge” two fold families. These “chameleon” proteins are sensitive to a small number of mutations that make these proteins part of one family or another. (b) An example of the chameleon proteins λ Cro (Protein DataBank access number: 5CRO) and P22 Cro (Protein DataBank access number: 1RZS) (Newlove et al., 2006): structural alignment of these two proteins demonstrates high structural similarity despite dramatic differences in their secondary structures.
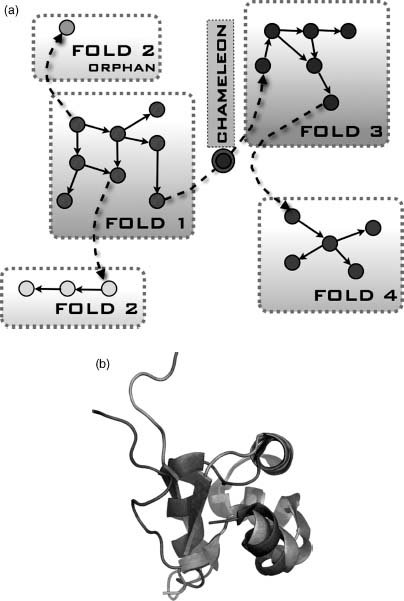
Figure 39.3. The first and the second largest PDUG subclusters. Representative structures for the first (upper graph) and the second largest (lower graph) subclusters of the PDUG are overlayed with the graphs. Figure also appears in the Color Figure section.
Examining the PDUG can give some support regarding whether convergent or divergent evolution is being utilized to create the current set of observed protein domains. The population of each of PDUG subcluster described above is observed to follow the power law distribution. However, the significance of this distribution is nullified when compared to a random graph (null hypothesis) that has been constructed to contain the identical number of nodes and edges found in PDUG. The control model showed the same distribution of members in fold families and therefore suggests that this distribution is a property of a random graph and do not have any further deep underlying meaning. On the contrary, the distribution of the connections between protein domains is very particular to PDUG when compare to a random graph. Using a simple model that accounts for divergent protein evolution with only two natural processes—gene duplications and point mutations—the observed distributions of domain connectivity can be reproduced (Dokholyan, Shakhnovich, and Shakhnovich, 2002) thus providing strong support for the divergent evolution theory (Figure 39.2).
In the protein domain evolution model presented by Dokholyan, Shakhnovich, and Shakhnovich (2002), proteins undergo gene duplications and new domains (paralogs and orthologs) accumulate point mutations over time (Figure 39.4). If these mutations do not significantly alter protein folding stability, that is, new proteins are stable enough to perform their functions, then they constitute the same fold. When a critical number of mutations accumulate, the core is potentially at risk to be disrupted or rearranged forcing significant structural changes, thereby giving birth to a new fold family. Within a fold family, sequences also diverge unequally: sequences defining homologues share 20% sequence similarity, while a fold family unifies numerous families of homologues with distinct numbers of homologue family members. Since the domain core preservation is an essential constraint in protein evolution, sequences with ~20% similarity are “guaranteed” to have structural similarity if the fraction of the shared residues constitute the critical component of the core. However, the conservation of the core may not be the only contributing factor effecting the distribution of fold families. Another contributing factor may be the physicochemical properties of the amino acids—the protein alphabet that defines protein sequence and structure. Next, we discuss the properties of the protein alphabet.
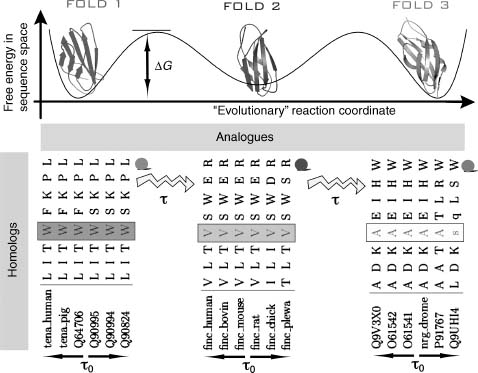
Figure 39.4. Schematic representation of the evolutionary processes that result in conservation patterns of amino acids. For a given family of folds, for example, immunoglobulin (Ig) fold in this schema, there are several minima (3) in the hypothetical free energy landscape in the sequence space as a function of the “evolutionary” reaction coordinate (such as time) (Dokholyan and Shakhnovich, 2005). Each of these minima are formed by mutations in protein sequences at typical time scales (τ0), that do not alter the protein’s thermodynamically and kinetically important sites, forming families of homologous proteins. Transitionsfrom one minimum to another occur at longer time scales τ= τ0 exp (ΔG/T), where ΔG is the free energy barrier separating one family of homologous proteins from another. At time scale t mutations occur that alter several amino acids at the important sites of the proteins so that the protein properties are not compromised, but the fold is changed. At time scale t the family of analogues is formed. Three minima in this schema represent three families of homologues (1TEN, 1FNF, and 1CFB) each comprised of six homologous proteins. Only eight positions in the aligned proteins are shown: from 18 to 28. It can be observed that at position 4 (marked by blocks) in each of the families presented in the diagram amino acids are conserved within each family of homologues, but vary between these families. This position corresponds to position 21 in Ig fold alignment (to 1TEN) and is highly conserved (Dokholyan and Shakhnovich, 2001). Modified from Dokholyan NV, Shakhnovich EI. Scale-Free Evolution: From Proteins to Organisms. In: Koonin EV, Wolf YI, Karev GP, eds. Power Laws, Scale-Free Networks and Genome Biology. Austin: Landes Bioscience, 2005.
PROTEIN ALPHABET
The protein structure-sequence relationship is determined by the amino acid
composition and amino acid order (see Chapter 2 for full details). The 20 amino acids have overlapping
physicochemical properties resulting in a redundancy of this set of building blocks. Hypothetically the
redundancy implies that proteins can be encoded with a smaller subset of the current amino acids. How
would be the minimum set of amino acid residues be? To make a crude approximation of the ideal alphabet
size, MI, we compare the number of available
sequences with this alphabet 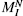 for a protein
of size N with the number of available protein conformations (z— 1)N—1 (estimated earlier in
Protein Structural Universe section), where z is the coordination number.
Equating these two numbers leads to MI ≈ z— 1 = 5. This result is very surprising because it is fourfold smaller
than the natural alphabet.
for a protein
of size N with the number of available protein conformations (z— 1)N—1 (estimated earlier in
Protein Structural Universe section), where z is the coordination number.
Equating these two numbers leads to MI ≈ z— 1 = 5. This result is very surprising because it is fourfold smaller
than the natural alphabet.
Although this estimation is extremely naive, a number of studies have supported similar estimates. First, using information theory and bioinformatics, Strait and Dewey showed that a typical protein sequence features Shannon entropy values of approximately 2.5 bits. This number means that one needs 22.5 ≈ 5.7 letters to encode protein structure. Of course, these letters are not amino acids, but rather a juxtaposition of various amino acids. Second, a study using lattice protein models and pairwise amino acid interaction potentials, demonstrated that one could design stable proteins using 20 but not 2 amino acid alphabet (Shakhnovich, 1994). The folding properties (foldability; Klimov and Thirumalai, 1996) of lattice protein models are also not significantly altered using a five-letter alphabet (Wang and Wang, 2000) but are altered using a two-letter alphabet. Third, by performing simulations of protein evolution, the amino acid conservation in protein families can be recapitulated using a six-letter amino acid alphabet (Dokholyan and Shakhnovich, 2001). Fourth, the SH3 domain can be experimentally redesigned to a sequence that consisted of only five amino acid types (Riddle et al., 1997); the expected probability of five-letter alphabet usage for a 56-residue protein is p ~ 10—29 (Dokholyan, 2004). Last but not least, the usage of amino acid types in natural proteins is less than expected if amino acids were chosen randomly with naturally occurring frequencies (Dokholyan, 2004). Taken together, it seems that Nature has utilized a larger alphabet than it could have for the protein universe.
Why does Nature exploit a larger alphabet than necessary for creating diversity in protein structure and function? Naively, it seems that a larger alphabet size would be inefficient because of the additional metabolic machinery that is needed by each additional amino acid. However, there are other important properties of natural proteins that are only possible with the current, and larger, set of amino acids. For examples, it is important to retain robustness in the protein structure. By creating diversity within the repertoire of amino acids, to the impact of potentially damaging mutations is reduced. If Nature utilized the most efficient “ideal” set of amino acids, then proteins are not safe guarded by mutations that would be damaging to protein folds.
Another benefit for having a larger alphabet size is that the evolutionary barriers (free energy barriers with respect to some “evolutionary” reaction coordinate—Figure 39.4) that separate fold families are lowered. This property allows Nature to optimally explore fold families in the course of protein evolution. Extremely large barriers, which would be a consequence if a reduced set of amino acids were used, would “freeze” the protein universe in one state and evolution would not be able to proceed. Hence, it is expected that as evolution proceeds, the alphabet size increases (Jordan et al., 2005), although not all amino acids may be utilized at any given point during evolution.
It is plausible that Nature chooses a golden mean between robustness (tolerance to mutations) and metabolic efficiency in selecting the protein alphabet size (Figure 39.5). The redundancy within the amino acid set also has important implications on protein design: it offers a margin for error associated with the inaccuracies inherent in the current force fields used by computer-based protein design. It also allows for the diversification of sequences without altering protein fold. Next, we describe the effects of alphabet size and other physical factors on the population of a given fold.
Figure 39.5. Hypothetical diagram of the benefits and drawbacks of protein alphabet size. The robustness associated with protein folds increases as the alphabet size M increases (dot-dashed line). At the same time, metabolic cost for producing M number of amino acids is also an increasing function of M (solid line). We posit that the latter function is a more rapidly growing one than that for the former. Two intercepts of these lines correspond to the critical (Mcrit) and the optimal (Mopt) alphabet sizes. The critical alphabet size signifies the point at which it becomes beneficial to produce proteins tolerant to mutations. The optimal alphabet size signifies the point at which the metabolic cost and robustness are at an optimal state, above which the metabolic cost outweighs the benefits of robustness of folds to mutations.
LESSONS FOR ENGINEERING STABLE PROTEINS
Protein stability is perhaps the most important determinant of protein evolution. In which case, what lessons for rational protein design could this observation teach us? The fold does provide constraints for the number of sequences that can adopt a given structure, but how would the number of available amino acids for use affect this number? What other physical factors contribute to protein designability? Next we attempt to shed light on these questions from a simplified physical consideration.
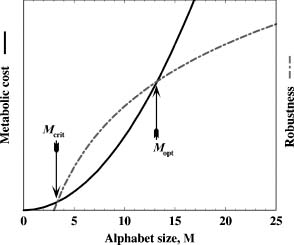
For a protein to be stable in its native state, the potential energy H(Γ) of its native state Γ must be smaller than that of any other alternative (decoy) state ΓD, for all decoys D:
(39.1)
Using the random energy model (Derrida, 1980), the thermodynamic stability of proteins and the potential energy difference (energy gap) ΔH between the native state and the lowest potential energy decoy ΓC can be related (Bryngelson and Wolynes, 1989; Gutin and Shakhnovich, 1993), which is then normalized by the root-mean-square deviation of the distribution of potential energies 0(H) of decoy conformations (Dokholyan, 2004):
Equation 39.2 provides a measure that helps to find a sequence S that minimizes the Z-score during the process of rational design.
This Z-score has been minimized to
find an ideal force field for a M-letter alphabet (Goldstein, Luthey-Schulten,
and Wolneys, 1992), and the actual value of the minimal Z-score value has
recently been derived, 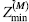 (Dokholyan, 2004):
(Dokholyan, 2004):
where N is a protein length, γ is an effective number of degrees of freedom per atom—a parameter that reflects protein flexibility (Dokholyan, 2004). The kernel function K (σa,σb) is
where fij are the frequencies of contacts between atoms i and j in decoy conformations, Δij is the contact matrix element, which is equalto1 or 0 depending on the presence of the contact between atoms i and j in the native state. si(σa) is the amino acid at the position i of type σa.
Furthermore, Eq. 39.3
takes on a simpler form when using the G ,
model (G
,
model (G , 1983), in which atomic
interactions are determined by the native protein structure (Dokholyan, 2004)
, 1983), in which atomic
interactions are determined by the native protein structure (Dokholyan, 2004)
Comparing Eqs 39.5 and 39.3, it is straightforward to prove that for all M
Equation 39.6
has profound implications on protein design: it suggests that with an increase of the size of available
protein alphabet, more stable proteins can be designed. The limiting case is theG model, in whichthe alphabetsizeis equal to the number of
possible contacts in a protein.
model, in whichthe alphabetsizeis equal to the number of
possible contacts in a protein.
Another important implication of Eqs 39.3 and 39.4 is that they can answer the question regarding the smallest alphabet size Mc required to encode a protein. Interestingly, this value
(39.7)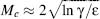
is independent of the protein length N (Dokholyan, 2004; ε is a factor independent of N and M). Thus, with an alphabet of size M ≥ Mc one can design a protein of arbitrary length.
The values of the Zmin suggest three principal factors that govern protein designability: (i) the alphabet size M, (ii) protein flexibility γ, and (iii) properties of the unfolded or misfolded states fij. The alphabet size determines the maximum possible stability of designed proteins and, therefore, how many sequences a given fold can adopt. The protein flexibility and unfolded states are important factors to account for during rational protein design as they differentiate the designed proteins from the reference states (decoys). Hence, proper sampling of protein conformations during computational protein design is essential.
An important consequence of Eqs 39.3-39.5, is that they suggest the concept of designability (Li et al., 1996), that is, that some folds may have more sequences that make them stable than others. Indeed, since the properties of unfolded or molten globule (unfolded with some compact units; Ptitsyn, 1995; Finkelstein and Ptitsyn, 2002) states are determined by the native state (Pappu, Srinivasan, and Rose, 2000; Fitzkee and Rose, 2004; Kohn et al., 2004; Ding, Jha, and Dokholyan, 2005), the frequencies of contacts fij impact Zmin. Hence, the lower the Zmin for a given fold, the more variation in stability due to mutations a given fold can tolerate, and the larger fold family we expect. England and Shakhnovich (2003) further uncovered role of the contact matrices on protein designability by deriving an explicit dependence of the number of designable sequence on the largest eigenvalue of the contact map.
The thermodynamic stability requirement has no implication for how stable natural proteins are (Taverna and Goldstein, 2002; Xia and Levitt, 2002). In fact, it has been established that natural proteins can be “redesigned” to be more stable than wild type (Chen et al., 2000; Dantas et al., 2003). Extremely stable proteins are not necessarily beneficial to Nature. As we show below, it is hard to evolve proteins to be extremely stable (whose Z-values are proximal to Zmin). Additionally, extremely stable proteins are maximally sensitive to random mutations. Hence, a majority of natural proteins are “marginally” stable (Taverna and Goldstein, 2002). As long as a protein optimally performs its function, there is no evolutionary pressure to make it more stable.
Theoretically, one can always improve the stability of a protein up to Zmin value for a corresponding fold. However, the thermodynamic stability of the original fold and the fold limiting value Zmin significantly affect the ability to find such sequences. To demonstrate this, let us note that the distribution of the Z-values of amino acid sequences that stabilize a given fold is normal. Indeed, it is an assumption of the Random Energy Model that the potential energy is a sum of “random” pairwise energy terms between atoms and, therefore, the values of potential energies of protein conformations follow a Gaussian distribution, which after normalization (Eq. 39.2) becomes normal. Hence, the number of sequences Ξ that are more stable than a given one with the Z-value equals to Z0:
(39.8)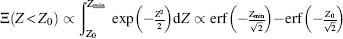
If the thermodynamic stability of a protein that we wish to redesign is proximal to a fold’s minimal value Zmin, the number of sequences becomes extremely hard to find as their number significantly decreases
Thus, the number of sequences more stable than a given one (with the Z-value equals to Z0) Ξ(Z < Z0) decreases dramatically as Z0 approaches its limiting value. This observation makes computational or experimental searches for sequences that make a protein even more stable an extremely difficult task.
An important implication of Eq.39.9 is that most random mutations are destabilizing. This consequence is especially important for many human diseases, suggesting that single nucleotide polymorphisms (SNPs) associated with diseases may decrease the stability of proteins produced from the corresponding genes. From this discussion, we can appreciate the limitation state structural stability has on shaping the allowable sequence space for a given fold.
PROTEIN ENGINEERING: US VERSUS NATURE
Learning how Nature operates has obvious advantages, but it is always important to remember the underlying motives for evolving or designing a specific protein. We often pursue goals that are distinct from Nature’s goals when designing proteins. For Nature it is important to design a functional protein. Proteins are not under evolutionary pressure to be extremely stable, more active than that is required for existing cell environments, or extremely fast folders. Most existing computational algorithms for protein design, on the other hand, search specifically for the sequence that minimizes the potential energy of a given scaffold. Although the ultimate goal of the protein design field is to rationally manipulate protein function and cell life, Nature evolves proteins as a part of the complex cellular system, thereby taking into consideration a whole spectrum of factors and functions. In this perspective, the future of the protein evolution field is projected into the realm of systems evolution.
There are many other constraints that Nature honors in the course of evolution. For example,
allostery is an important factor to account for protein function. It is currently extremely difficult to
account for allosteric effects in proteins during rational design. Some success has been achieved with
designing molecular switches (Ambroggio and Kuhlman, 2006). However, nobody has so far succeeded with
the design of rational changes in protein structure upon ligand binding. This problem is one of the most
complex in protein design since it requires design of networks of amino acid interactions throughout
protein structure. While the communication of amino acids within protein structures has been
establishedusing graph theoretical analysis in anumber of studies (Lockless and Ranganathan, 1999;
Dokholyan et al., 2002; Vendruscolo et al., 2002), it is not clear whether it is purposely evolved or
just a generic property of protein structure. For example, while there is a clear relation between
topologically and kinetically important residues in proteins (Dokholyan et al., 2002; Vendruscolo et
al., 2002), this relation may be a consequence of a similar one between protein structure and its
folding kinetics. This observation is supported by several studies that identified significantly
contributing residues to protein folding kinetics (Clementi, Nymeyer, and Onuchic, 2000; Ding et al.,
2002a) using a structure-based model of protein energetics the G model (G
model (G , 1983).
Thus, the success in designing allostery in proteins strongly depends on the significant progress in our
understanding of amino acid interaction networks in protein structure and their evolution.
, 1983).
Thus, the success in designing allostery in proteins strongly depends on the significant progress in our
understanding of amino acid interaction networks in protein structure and their evolution.
The function of some proteins is structurally achieved by disordered regions that lack secondary or any well-defined unique structure. In fact, there are a number of fully disordered proteins (Le Gall et al., 2007) and their potential impact on protein function, biology, and other functional roles are discussed in Chapter 38. Computational design of such proteins is a formidable challenge. Perhaps what makes rational design of disordered proteins even more complex is that despite the lack of well-defined structure of such proteins, they are distinct from random polymers. These proteins coexist in multiple states, which actually have unique structural properties at the ensemble level, that is, they share specific structural signatures. One remarkable example is a-synuclein, which lacks a unique native state, but is more compact than would be expected for a random polypeptide (Dedmon et al., 2005). Although the function of α-synuclein is unknown, disordered regions are often employed by other proteins, such as antibodies and cell signaling proteins, which have intrinsic plasticity to recognize and bind other molecules. In such proteins, disorder is only visible in free structure. Local or global structural reorganization occurs upon the binding of partner molecules. Such proteins are a significant complication for computational protein design because the stability of the complex with a partner protein, rather than the thermodynamic stability of free proteins, is the priority for Nature. Since many such proteins have a large number of partners, a further challenge for protein design is to engineer protein interactions with several of the partners, which may force a designed protein to adopt a number of alternative bound structures.
Another important focus of natural design is the active site of enzymes. Enzyme activity is extremely sensitive to the geometry and dynamic properties of the active site and its conformation in the transition states. This sensitivity is controlled at the sub-Angstrom level, making Nature the most elegant and scrupulous designer. The level of accuracy required for enzyme design makes it one of the most challenging tasks for protein designers. Although there has been significant progress in computational enzyme design, pioneered by Hellinga (Dwyer et al., 2004), we are still not in the realm of natural enzyme design.
Besides the differences in design philosophies between Nature and us, there are a number of other issues that we need to overcome to become efficient in designing functional proteins. In the next section, we discuss some of these issues.
CHALLENGES IN PROTEIN DESIGN
There are a number of experimental and computational approaches to protein design. While experimental approaches that attempt to mimic evolution in vitro offer a powerful search methodology for desired proteins, computational design has particular appeal since it provides rational explanation, and correspondingly a higher perspective for control, for the effect of changes on protein structure and function. Next, we discuss the main difficulties facing computational protein design.
Energetics
One of the most important components in protein design, as well as protein folding and structure prediction, is the force field. The force field is a set of parameters that contributes to the calculation of the potential energy of the protein. There are a number of strategies to derive a force field for a given molecular model: physical, empirical, knowledge based, constraint based, and their combinations. Physical force fields (e.g., CHARMM and Amber) require physical entities, that is, atoms, and therefore are most appropriate for detailed all-atom models. Empirical force fields rely on specific observations pertinent to a given molecule, and therefore are molecule type-specific. Among empirical force fields is the structure-based Goo model, which biases proteins to their native states. Knowledge-based force fields are constructed on current knowledge of molecular structure, physical/chemical properties, and evolution, and therefore are limited to molecules that resemble known molecules. Constraint-based force fields rely on experimental data, molecular structure, and dynamics.
The more details of interactions accounted by the force field (i.e., the more accurate it is), the slower the calculation of the potential energy of a given protein state. Slow computation of the potential energy, in turn, results in diminished sampling or search abilities, whether it is a search for a protein sequence during protein design, or conformational sampling during protein folding or structure prediction. Hence, there is a fine balance between the accuracy of the force field and the ability to search or sample. Finding such a balance between the potential energy calculations and the ability to search for a solution is one of the principal challenges in protein design.
Conformational sampling is the other side of the coin from estimating the free energy of a given protein state and its corresponding thermodynamic stability. The free energy estimation of a given state requires understanding the properties of the ensemble of all conformations in the free energy basin of a state of interest. During protein design, one needs to find a large number of conformations that a given sequence can adopt within such a basin. An amino acid substitution may result in atomic clashes between the newly substituted amino acid and other residues (Ding and Dokholyan, 2006; Yin et al., 2007). Such clashes can be resolved by “massaging” the protein structure via conformational sampling of the protein backbone. Surprisingly the perturbation of the backbone required for resolving a clash is often very minimal, less than 1 Å (Yin et al., 2007), although it is important to note that not all clashes can be resolved.
Estimation of protein thermodynamic stabilities is even more challenging as it requires the knowledge of the free energies of the reference (unfolded) states. The free energy of the unfolded states is predominantly determined by the accurate modeling of the ensembles of unfolded state structures. Due to difficulties in determining the ensemble of unfolded states, many design algorithms rely on approximations of the reference states or derive these parameters by training using various strategies. Rapid sampling techniques may potentially improve thermodynamic stability evaluations through explicit sampling (Ding, Jha, and Dokholyan, 2005).
Alternative Binding Sites
An important potential complication during design of protein-protein interactions is the presence of alternative binding sites. Even though interactions at the alternative binding sites are most likely to occur at lower affinity, these sites compete for the ligand and, therefore, decrease the effective binding to the target region. These complications could be alleviated by (1) improving sampling during docking of a target protein on a scaffold to identify the potential alternative binding sites, and (2) performing negative design to decrease binding affinities at the alternative binding sites.
Aggregation
Protein aggregation due to association of identical proteins is a common phenomenon and can result from multiple factors. Protein aggregation occurs when protein thermodynamic stability and concentration are such that identical species can form intermolecular hydrogen bonds between their backbones. Thermodynamic stability plays an essential role in protein aggregation, as proteins often need to unfold to expose their backbone to other proteins for hydrogen bond formation (Ding et al., 2002b).
There are two dominant reasons for protein aggregation in the course of protein design. First, the designed protein may not be stable enough. In such cases, further improvement of the protein’s thermodynamic stability may alleviate the problem. Second, if the protein is rich in β-sheets, the amino acids constituting these β-strands are already in geometrical configurations consistent with those of protein aggregates. This is a serious complication during protein design as there is no clear understanding, despite a number of interesting considerations showing how Nature protects β-rich proteins from aggregation (Patki, Hausrath, and Cordes, 2006; Richardson and Richardson, 2002). It has been suggested that capping β-sheets with charged residues and creating bulges on the surface of β-sheets may protect them from associating with identical proteins. However, no successful design has been carried out to build a novel β-rich protein. Further understanding of Nature’s defense against protein aggregation may offer new strategies for designing β-rich proteins.
CONCLUSIONS
Protein engineering enters a new era as rational manipulation of protein structure becomes more successful due to acquired knowledge about protein structure, energetics, and evolution. With the increase of the number of determined protein structures, we now better understand the organization of the protein structure universe. We are able to link structurally diverse protein families and understand evolutionary determinants of families of protein structures. By developing an understanding of the basic mechanisms of protein evolution, we learn to manipulate protein structure by mimicking the natural processes. From theoretical considerations, we have learned important lessons for engineering stable proteins, such as the protein alphabet size, protein flexibility, and the properties of the unfolded states.
Despite tremendous progress in protein engineering, we still face challenges. These challenges include design in the framework of cellular environments, for example when protein design must include potentially negative design against interactions with other proteins. Modeling unfolding proteins is essential to protein design and improvements in our models of unfolded states may allow for rational manipulations of naturally disordered proteins or proteins that feature functional unstructured regions. Further challenges are associated with sub-angstrom design that is necessary for building novel enzymes. Understanding protein aggregation will help us defy such natural phenomena as protein aggregation and nonspecific associations with other proteins.
Improvements may come from further development of the force fields and our ability to more exhaustively sample protein conformations. An understanding of the protein alphabet is important to computational protein design (Shakhnovich, 1998) because the underlying protein alphabet determines the parameter set for the energy function that is used for protein design. Therefore, further studies are needed to uncover the fundamental protein alphabet responsible for encoding protein three-dimensional structure. These studies may also shed light on the redundancy of the genetic code and identify the principal rules of molecular evolution.
Protein engineering is already influencing modern biology and offering help in understanding cellular life. Many of these considerations are applicable to other polymers, such as RNA and DNA molecules. Although these molecules have specific challenges associated with their design, most of the discussed aspects of protein design are also applicable to these molecules. Future engineering efforts offer remarkable promise for impacting medicine: from the engineering of antibodies and enzymes to the development of biomarkers for early diagnosis of disease. Protein engineering will also play an important role in elucidating the molecular etiologies of human diseases and the development of personalized medicine.